Simulation and Modelling - Old Questions
2. Use multiplicative congruential method to generate a sequence of three digits random numbers between (0, 1) with X0=27, a=3 and m=1000. Use any one of the uniformity test to find out whether the generated numbers are uniformly distributed or not? (Critical value for α=0.05 and N=5 is 0.565).
Answer
AI is thinking...
Given,
X0 = 27,
α = 3,
m=1000
We have,
For multiplicative congruential method:
Xi+1 = (α Xi ) mod m
& Ri =Xi/m,
The sequence of random numbers are calculated as follows:
X0 = 27
R0 = 27/1000 = 0.027
X1 = (α X0) mod m = (3*27) mod 1000 = 81 mod 1000 = 81
R1 = 81/1000 = 0.081
X2 = (α X1) mod m = (3*81) mod 1000 = 243 mod 1000 = 243
R2 = 243/1000 = 0.243
X3 = (α X2) mod m = (3*243) mod 1000 = 729 mod 1000 = 729
R3 = 729/1000 = 0.729
X4= (α X3 ) mod m = (3*729) mod 1000 = 2187 mod 1000 = 187
R4 = 187/1000 = 0.187
Arranging the above random numbers number in ascending order:
0.027, 0.081, 0.187, 0.243,, 0.729
Here, N = 5
Calculation table for Kolmogorov-Smirnov test :
| i | ||||
| 1 | 0.027 | 0.2 | 0.173 | 0.027 |
| 2 | 0.081 | 0.4 | 0.319 | - |
| 3 | 0.187 | 0.6 | 0.413 | - |
| 4 | 0.243 | 0.8 | 0.557 | - |
| 5 | 0.729 | 1 | 0.271 | - |
Now, calculating
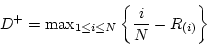 = 0.557
= 0.557
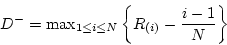 = 0.027
= 0.027
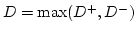 = 0.557
= 0.557
Given, Critical value 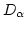 = 0.565
= 0.565
Since the computed value, D = 0.557, is less than the tabulated critical value, 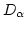 = 0.565, the hypothesis of no difference between the distribution of the generated numbers and the uniform distribution is not rejected.
= 0.565, the hypothesis of no difference between the distribution of the generated numbers and the uniform distribution is not rejected.