Data Structures and Algorithms 2066

#include<stdio.h>

#include<conio.h>

#define SIZE 10

void push(int);

void pop();

void display();

int stack[SIZE], top = -1;

void main()

{

   int value, choice;

   clrscr();

   while(1){

      printf("\\n\\n***** MENU *****\\n");

      printf("1. Push\\n2. Pop\\n3. Display\\n4. Exit");

      printf("\\nEnter your choice: ");

      scanf("%d",&choice);

      switch(choice){

          case 1: printf("Enter the value to be insert: ");

                  scanf("%d",&value);

                  push(value);

                  break;

          case 2: pop();

                  break;

          case 3: display();

                  break;

          case 4: exit(0);

          default: printf("\\nWrong selection!!! Try again!!!");

      }

   }

}

void push(int value){

   if(top == SIZE-1)

      printf("\\nStack is Full!!! Insertion is not possible!!!");

   else{

      top++;

      stack[top] = value;

      printf("\\nInsertion success!!!");

   }

}

void pop(){

   if(top == -1)

      printf("\\nStack is Empty!!! Deletion is not possible!!!");

   else{

      printf("\\nDeleted : %d", stack[top]);

      top--;

   }

}

void display(){

   if(top == -1)

      printf("\\nStack is Empty!!!");

   else{

      int i;

      printf("\\nStack elements are:\\n");

      for(i=top; i>=0; i--)

          printf("%d\\n",stack[i]);

   }

}

Merits of Contiguous List / array

• It is used to represent multiple data items of same type by using only single name.

• It can be used to implement other data structures like linked lists, stacks, queues, trees, graphs etc.

• 2D arrays are used to represent matrices.

• Implementation of list using array is easier as compared other implementation.

Demerits of Contiguous List / array

• The size of the array is fixed. Most often this size is specified at compile time. This makes the programmers to allocate arrays, which seems "large enough" than required.

• Inserting new elements at the front is potentially expensive because existing elements need to be shifted over to make room.

• Deleting an element from an array is not possible. Linked lists have their own strengths and weaknesses, but they happen to be strong where arrays are weak.

• Generally array's allocates the memory for all its elements in one block whereas linked lists use an entirely different strategy. Linked lists allocate memory for each element separately and only when necessary.

Merits of Linked List

1. Linked lists are dynamic data structures. i.e., they can grow or shrink during the execution of a program.

2. Linked lists have efficient memory utilization. Here, memory is not preallocated. Memory is allocated whenever it is required and it is de-allocated (removed) when it is no longer needed.

3. Insertion and Deletions are easier and efficient. Linked lists provide flexibility in inserting a data item at a specified position and deletion of the data item from the given position.

4. Many complex applications can be easily carried out with linked lists.

5. There is no need to define an initial size for a Linked list.

6. Linked List reduces the access time.

Demerits of Linked List

1. They use more memory than arrays because of the storage used by their pointers.

2. Difficulties arise in linked lists when it comes to reverse traversing. For instance, singly linked lists are cumbersome to navigate backwards and while doubly linked lists are somewhat easier to read, memory is wasted in allocating space for a back-pointer.

3. Nodes in a linked list must be read in order from the beginning as linked lists are inherently sequential access.

4. Nodes are stored in-contiguously, greatly increasing the time required to access individual elements within the list, especially with a CPU cache.

Singly linked list is a sequence of elements in which every element has link to its next element in the sequence. For e.g. the following example is a singly linked list that contains three elements 12, 99, & 37.

Steps involved in inserting a node at the beginning of singly linked list:

let *head be the pointer to first node in the current list

1. Create a new node using malloc function

        NewNode=(NodeType*)malloc(sizeof(NodeType));

2. Assign data to the info field of new node

        NewNode->info=newItem;

3. Set next of new node to head

        NewNode->next=head;

4. Set the head pointer to the new node

        head=NewNode;

5. End

Steps involved in inserting a node at the end of the singly linked list:

let *head be the pointer to first node in the current list

1. Create a new node using malloc function

        NewNode=(NodeType*)malloc(sizeof(NodeType));

2. Assign data to the info field of new node

        NewNode->info=newItem;

3. Set next of new node to NULL

        NewNode->next=NULL;

4. if (head ==NULL)then

        Set head =NewNode.and exit.

5. Set temp=head;

6 while(temp->next!=NULL)

        temp=temp->next;     //increment temp

7. Set temp->next=NewNode;

8. End

Steps involved in deleting the first node of singly linked list:

let *head be the pointer to first node in the current list

1. If(head==NULL) then

        print “Void deletion” and exit

2. Store the address of first node in a temporary variable temp.

        temp=head;

3. Set head to next of head.

        head=head->next;

4. Free the memory reserved by temp variable.

        free(temp);

5. End

Steps involved in deleting the last node of singly linked list:

let *head be the pointer to first node in the current list

1. If(head==NULL) then //if list is empty

        print “Void deletion” and exit

2. else if(head->next==NULL) then //if list has only one node

        Set temp=head;

        print deleted item as,

        printf(“%d” ,head->info);

        head=NULL;

        free(temp);

3. else

        set temp=head;

        while(temp->next->next!=NULL)

            set temp=temp->next;

        End of while

        free(temp->next);

Set temp->next=NULL;

4. End

Given,

In-order : VPNAQRSOKBTM

Pre-order : SPVQNARTOKBM

In a Preorder sequence, leftmost element is the root of the tree. So we know ‘S’ is root for given sequences. By searching ‘S’ in In-order sequence, we can find out all elements on left side of ‘S’ are in left subtree and elements on right are in right subtree. So we know below structure now.

Among VPNAQR, P appears first in pre-order so it is root of left subtree. 

Now, we recursively follow above steps for left subtree:

_______________

Among OKBTM, T appears first in pre-order so it is root of right subtree.

Now, we recursively follow above steps for right subtree:

_______________

Which is the required binary tree.

Function call:

   transfer ( 3, "R‟, "L‟, „"C‟);

Output:

Move Disk 1 from R to L

Move Disk 2 from R to C

Move Disk 1 from L to C

Move Disk 3 from R to L

Move Disk 1 from C to R

Move Disk 2 from C to L

Move Disk 1 from R to L

It can be shown in figure as:

void display()

{

   if(front == -1)

      printf("\\nCircular Queue is Empty!!!\\n");

   else{

      int i = front;

      printf("\\nCircular Queue Elements are : \\n");

      if(front <= rear){

         while(i <= rear)

            printf("%d\\t",cQueue[i++]);

      }

      else{

         while(i <= SIZE - 1)

            printf("%d\\t", cQueue[i++]);

         i = 0;

         while(i <= rear)

            printf("%d\\t",cQueue[i++]);

      }

   }

}

Divide-and-conquer algorithm breaks a problem into subproblems that are similar to the original problem, recursively solves the subproblems, and finally combines the solutions to the subproblems to solve the original problem.

Divide and Conquer algorithm consists of the following three steps.

1. Divide: Divide the original problem into a set of subproblems.
2. Conquer: Solve every subproblem individually, recursively.
3. Combine: Put together the solutions of the subproblems to get the solution to the whole problem.

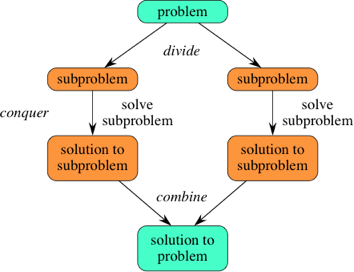
Merge sort works on the basis of divide and conquer algorithm. The basic concept of merge sort is divides the list into two smaller sub-lists of approximately equal size. Recursively repeat this procedure till only one element is left in the sub-list. After this, various sorted sub-lists are merged to form sorted parent list. This process goes on recursively till the original sorted list arrived.

Procedure for Merge sort:

To sort A[l…………r]

1.      Divide step: If a given array A has zero or one element, simply return; it is already sorted. Otherwise split A[l……….r] into two sub-arrays A[l………q] and A[q+1…………r] each containing about half of the element A[l…….r]. that is q is the half of way point of A[l…….r].

2.      Conquer step: Sorting the two sub-arrays A[l………q] and A[q+1…………r] recursively. When the size of sequence of is 1 there is nothing more to do.

3.      Combine step: Combine the two sub-arrays A[l……q] and A[q+1…………r] into a sorted sequence.

Given:

 21, 36, 56, 79, 101, 123, 142, 203

Now,

Tracing binary search for given data;

Set L=0, R=7, key=123 (search for 123)

Therefore, search successful and key(123) is at position (Mid+1)=5+1=6.

Again,

 L=0, R=14, key=153 (search for 153)

  Therefore, search failure and key(153) is not present in the given list.

Difference between tree and graph

Spanning Tree

A spanning tree is a subset of Graph G, which has all the vertices covered with minimum possible number of edges. Hence, a spanning tree does not have cycles and it cannot be disconnected.

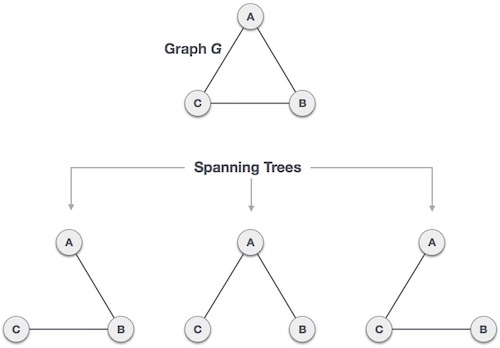
Spanning Forest

Spanning forest is a forest that contains every vertex of G such that two vertices are in the same tree of the forest when there is a path in G between these two vertices.

--> Spanning forest is a forest of spanning tree in the sub-graph of G.

MST (Minimum cost Spanning Tree) problem

A minimum spanning tree (MST) is a spanning tree that has minimum weight than all other spanning trees of the same graph.

There are three different algorithms to construct the minimum spanning tree:

•     Prim’s algorithm: Grows the tree in stages. Selects an edge with lowest cost that can be added to the tree without forming cycle.
•     Kruskal’s algorithm: In each stage select the edge in non-decreasing order of cost.
•     Sollin’s algorithm: Select several edges at each stage.

Given character and their frequencies:

Now sort these characters according to their frequencies in non-decreasing order.

The Huffman tree constructed for the above data is shown below:

Now from variable length code we get following code sequence.

Thus after using Huffman algorithm the total number of bits required is

= 48*1+11*3+9*4+14*3+7*4+11*3= 220 bits

Big-O notation signifies the relationship between the input to the algorithm and the steps required to execute the algorithm.

A function f(n) is said to be “big-Oh of  g(n)” and we write, f(n)=O(g(n)) or simply f=O(g), if there are two positive constants c and n0 such that f(n)<=c*g(n) for all n>=n0.

E.g. The big oh notation of  f(n)=n+4 is O(n) since n+4<=2n for all n>=4.

The big oh notation of  f(n)=n2+3n+4 is O(n2) since n2+3n+4<=2n2  for all n>=4.

Big O notation specifically describes worst case scenario. It represents the upper bound running time complexity of an algorithm.

Quick-Sort vs Merge-Sort

Merge sort is more efficient and works faster than quick sort in case of larger array size or datasets.
whereas
Quick sort is more efficient and works faster than merge sort in case of smaller array size or datasets.

Merge sort has the following performance characteristics:

• Best case: O(n log n)
• Average case: O(n log n)
• Worst case: O(n log n)

Quicksort has the following performance characteristics:

• Best case: O(n)
• Average case: O(n log n)
• Worst case: O(n2)

Circular Linked List (CLL)

Circular linked list is a sequence of elements in which every element has link to its next element in the sequence and the last element has a link to the first element in the sequence.

Example:

Circular list has no end.

In a circular linked list there are two methods to know if a node is the first node or not.

• Either a external pointer, list, points the first node or
• A header node is placed as the first node of the circular list.

Doubly Linked List (DLL)

Doubly linked list is a sequence of elements in which every element has links to its previous element and next element in the sequence.

In double linked list, every node has link to its previous node and next node. So, we can traverse forward by using next field and can traverse backward by using previous field. Every node in a double linked list contains three fields and they are shown in the following figure...

Here, 'link1' field is used to store the address of the previous node in the sequence, 'link2' field is used to store the address of the next node in the sequence and 'data' field is used to store the actual value of that node.

Example:

Doubly Circular Linked List (DCLL)

A circular doubly linked list is one which has the successor and predecessor pointer in circular manner. It is a doubly linked list where the next link of last node points to the first node and previous link of first node points to last node of the list. E.g.

a) Hash Function

Hashing is a well-known technique to search any particular element among several elements. It minimizes the number of comparisons while performing the search. 

In hashing, an array data structure called as Hash table is used to store the data items. Hash table is a data structure used for storing and retrieving data very quickly. Insertion of data in the hash table is based on the key value. Hence every entry in the hash table is associated with some key. Using the hash key the required piece of data can be searched in the hash table by few or more key comparisons.

    Fig: Hashing Mechanism

Hash function is a function which is used to put the data in the hash table. Hence one can use the same hash function to retrieve the data from the hash table. Thus hash function is used to implement the hash table. The integer returned by the hash function is called hash key.

b) External Sorting

Sorting large amount of data requires external or secondary memory. This process uses external memory such as HDD, to store the data which is not fit into the main memory. So primary memory holds the currently being sorted data only. All external sorts are based on process of merging. Different parts of data are sorted separately and merging together. For e.g. merge sort

c) ADT

Abstract data types are a set of data values and associated operations that are precisely independent of any particular implementation. Generally the associated operations are abstract methods. E.g. stack, queue etc.