Compiler Design and Construction 2072
Attempt all questions. (10x6=60)
AI is thinking...
1. Explain the analysis phase of the compiling a source program with example.
Analysis phase breaks up the source program into constituent pieces and creates an intermediate representation of the source program. Analysis of source program includes: lexical analysis, syntax analysis and semantic analysis.
Block diagram for phases of compiler:
1. Lexical Analysis:
In this phase, lexical analyzer reads the source program and returns the tokens of the source program. Token is a sequence of characters that can be treated as a single logical entity (such as identifier, operators, keywords, constants etc.).
2. Syntax Analysis:
In this phase, the syntax analyzer takes the token produced by lexical analyzer as input and generates a parse tree as output. In syntax analysis phase, the parser checks that the expression made by the token is syntactically correct or not, according to the rules that define the syntax of the source language.
3. Semantic Analysis:
In this phase, the semantic analyzer checks the source program for semantic errors and collects the type information for the code generation. Semantic analyzer checks whether they form a sensible set of instructions in the programming language or not. Type-checking is an important part of semantic analyzer.
Example of Analysis phase:
AI is thinking...
2. What are the functional responsibilities of a lexical analyzer? Write a lexical analyzer that recognizes the identifier of C language.
Lexical Analyzer reads the input characters of the source program, groups them into lexemes, and produces a sequence of tokens for each lexeme. The tokens are then sent to the parser for syntax analysis.
Responsibilities of a lexical analyzer are:
- It reads the input character and produces output sequence of tokens that the Parser uses for syntax analysis.
- Lexical analyzer helps to identify token into the symbol table.
- Lexical Analyzer is also responsible for eliminating comments and white spaces from the source program.
- It also generates lexical errors.
- Lexical analyzer is used by web browsers to format and display a web page with the help of parsed data from JavsScript, HTML, CSS
Second part:
/* Lex program to recognize the identifier of C language */
AI is thinking...
3. What are regular definitions? Given the following CFG,
Write the regular definitions for
the terminals used. Also, construct the transition diagram for id and num.
If Σ is an alphabet of basic symbols, then a regular definition is a sequence of definition of the form
d1 → r1
d2 → r2
.....
dn → rn
where, di is a distinct name and ri is a regular expression over symbols in Σ ∪ {d1, d2, ...., di-1}
Now,
Regular definitions for the terminals used in given grammar are:
digit → [0-9]
num → digit+(. digit+)?(E[+|-]? digit+)?
letter → [A-Za-z]
id → letter ( letter | digit )*
if → if
then → then
else → else
relop → < | > | <= | >= | = | <>Transition diagram for id:

Here 9, 10 & 11 are the name of states.
Transition diagram for num:
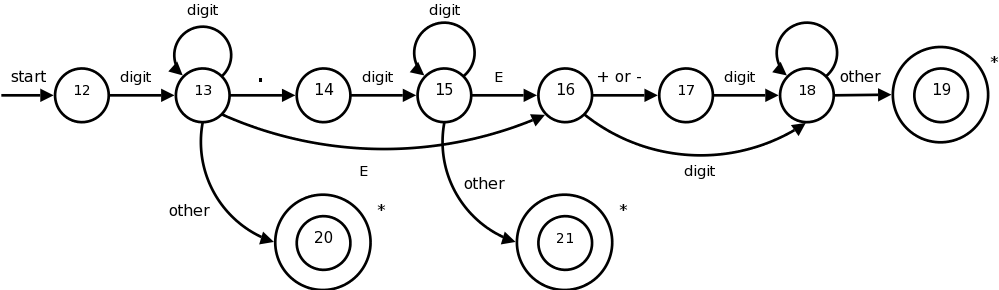
AI is thinking...
4. Given a regular expression (a+∈) bc*. Construct the DFA recognizing the pattern described by the regular expression using syntax tree based reduction.
Given RE;
(a+∈) bc*
The augmented RE of the given RE is:
(a+∈) bc* #
Syntax tree for augmented R.E. is
Calculating followpos:
followpos(1) = {2}
followpos(2) = {3, 4}
followpos(3) = {3, 4}
Now,
1) Start state of DFA = firstpos(root) = {1, 2} = S0
Use followpos of symbol representing position in RE to obtain the next state of DFA.
2) From S0 = {1, 2}
1 represents 'a'
2 represents 'b'
followpos(1) = {2} = S1
δ(s0, a) = S1
followpos(2) = {3, 4} = S2
δ(S0, b) = S2
3) From S1 = {2}
Here 2 represents 'b'
followpos(2) = {3, 4} = S2
δ(S1, b) = S2
4) From S2 = {3, 4}
Here 3 represents 'c'
4 represents '#'
followpos(3) = {3, 4} = S2
δ(S2, c) = S2
Now there was no new states occur.
Therefore, Final state = {S2}
Now the resulting DFA of given regular expression is:
AI is thinking...
5. Explain in detail about the recursive-descent parsing with example.
Recursive decent parsing is a top-down parsing technique that uses a set of recursive procedure to scan its input from left to right. It may involve backtracking. It starts from the root node (start symbol) and use the first production, match the input string against the production rules and if there is no match backtrack and apply another rule.
Rules:
1. Use two pointers iptr for pointing the input symbol to be read and optr for pointing the symbol of output string that is initially start symbol S.
2. If the symbol pointed by optr is non-terminal use the first production rule for expansion.
3. While the symbol pointed by iptr and optr is same increment the both pointers.
4. The loop at the above step terminates when
a. A non-terminal is encountered in output
b. The end of input is reached.
c. Symbol pointed by iptr and optr is unmatched.
5. If 'a' is true, expand the non-terminal using the first rule and goto step 2
6. If 'b' is true, terminate with success
7. If 'c' is true, decrement both the pointers to the place of last non-terminal expansion and use the next production rule for non-terminal
8. If there is no more production and 'b' is not true report error.
Example:
Consider a grammar
S → cAd
A → ab | a
Input string is “cad”
Initially, iptr = optr = 0
|
Input |
Output |
Rules Fired |
|
iptr(cad) |
optr(S) |
Try S → cAd |
|
iptr(cad) |
optr(cAd) |
Match c |
|
c
iptr(ad) |
c
optr(Ad) |
Try A → ab |
|
c
iptr(ad) |
c
optr(abd) |
Match a |
|
ca
iptr(d) |
ca
optr(bd) |
dead end, backtrack |
|
c
iptr(ad) |
c
optr(Ad) |
Try A → a |
|
c
iptr(ad) |
c
optr(ad) |
Match a |
|
ca
iptr(d) |
ca
optr(d) |
Match d |
|
cad
iptr(eof) |
cad
optr(eof) |
|
|
Parsing completed. |
|
|
AI is thinking...
6. Given the following grammar:
Given Grammar;
Now, Calculating First and Follow:
FIRST
First(E) = First(T) = First(F) = { (, id }
First(E’) = { +, ∈ }
First(T’) = { *, ∈ }
FOLLOW
Follow(E) = { ), $}
Follow(E’) = { ), $}
Follow(F) = { *, +, ), $ }
Follow(T) = { +, ) , $}
Follow(T’) = { +, ) , $}
Now, the Parsing table for given grammar is as below:
AI is thinking...
7. Define the term ‘item’, ‘closure’ and ‘goto’ used in LR parsing. Compute the SLR DFA for the following grammar.
Item
An “item” is a production rule that contains a dot(.) somewhere in the right side of the production. For example, A→ .αAβ , A→ α.Aβ, A→ αA.β, A→ αAβ. are items if there is a production A→ αAβ in the grammar.
Closure
If I is a set of items for a grammar G, then closure(I) is the set of LR(0) items constructed from I using the following rules:
1. Initially, every item in I is added to closure(I).
2. If A→ α.Bβ is in closure(I) and B →γ is a production, then add the item B → .γ to I if it is not already there.
Apply this rule until no more new items can be added to closure(I).
goto
If I is a set of LR(0) items and X is a grammar symbol (terminal or non-terminal), then goto(I, X) is defined as follows:
If A → α•Xβ in I then every item in closure({A → αX•β}) will be in goto(I, X).
Now,
The augmented grammar of the given grammar is,
S‘ → S
S → CC
C → aC | b
Next, we obtain the canonical collection of sets of LR(0) items, as follows,
I0 = closure ({S‘ → •S}) = {S‘ → •S, S → •CC, C → •aC, C → •b}
goto (I0, S) = closure ({S‘ → S•}) = {S‘ → S•} = I1
goto (I0, C) = closure ({S → C•C}) = {S → C•C, C → •aC, C→ •b} = I2
goto (I0, a) = closure ({C→ a•C}) = {C → a•C, C → •aC, C → •b} = I3
goto (I0, b) = closure ({C → b•}) = {C → b•} = I4
goto (I2, C) = closure ({S → CC•}) = {S → CC•} = I5
goto (I2, a) = closure ({C → a•C}) = {C → a•C, C → •aC, C → •b} = I3
goto (I2, b) = closure ({C → b•}) = {C → b•} = I4
goto (I3, C) = closure ({C → aC•}) = {C → aC•} = I6
goto (I3, a) = closure ({C → a•C}) = {C→ a•C, C → •aC, C → •b} = I3
goto (I3, b) = closure ({C → b•}) = {C → b•} = I4
Now, the SLR DFA of the given grammar is:
AI is thinking...
8. For the following grammar,
First part:
E → E + E {E.val = E1.val + E2.val}
E → E * E {E.val = E1.val * E2.val}
E → (E) {E.val = E1.val}
E →id {E.val = id.lexval}
Second part:
Removing left recursion as,
E → (E)R | id R
R → +ER1 | *ER1 | ε
Now add the attributes within this non-left recursive grammar as,
E → (E) {R.in = E1.val}R {E.val = R.s}
E →id {R.in = id.lexval} R1 { E.val = R.s}
R → +E {R1.in = E.val+R.in}R1 {R.s = R1.s}
R → *E { R1.in = E.val*R.in }R1 { R.s = R1.s }
R → ε { R.s = R.in}
AI is thinking...
9. Consider the following grammar for arithmetic expression using an operator ‘op’ to integer or real numbers.
E → E1 op E2 | num.num
| num | id
E → id { E.type = lookup(id.entry)}
E → num
{E.type = integer }
E → num.num { E.type = real}
E → E1 op E2 { E.type =
if(E1.type = integer and E2.type = integer)
then integer
else if (E1.type = integer and E2.type
= real)
then real
else if (E1.type = real and E2.type =
integer)
then real
else if (E1.type = real and E2.type =
real)
then real
else type_error()
}
AI is thinking...
10. What is three address code? Translate the expression a = b * - c + b * - c in to three address code statement.
The address code that uses at most three addresses, two for operands and one for result is called three address code. Each instruction in three address code can be described as a 4-tuple: (operator, operand1, operand2, result).
A quadruple (Three address code) is of the form: x = y op z where x, y and z are names, constants or compiler-generated temporaries and op is any operator.
Followings are the 3-address code statements for different statements.
- Assignment statement:
x = y op z ( binary operator op)
x = op y ( unary operator op)
- Copy statement: x = z
- Unconditional jump: goto L ( jump to label L)
- Conditional jump: if x relop y goto L
- Procedure call:
param x1
param x2
. .
..
param xn
call p, n i.e. call procedure P(x1,x2,….. xn)
- Indexed assignment:
x = y[i]
x[i] = y
- Address and pointer assignments:
x = &y
x = *y
*x = y
Given expression
a = b * - c + b * - c
The three address code of given statement is given below:
t1 = -c
t2 = b * t1
t3 = -c
t4 = b * t3
t5 = t2 + t4
a = t5
AI is thinking...